Calculating the dynamics

The down and orbit channels may not move during a flushing process, otherwise error ID 50927 is output. For this reason, the escape channel can take up 100% of the axis dynamics during a jump instead of the usual 50% per channel for die sinking.

The dynamics calculation can be separated into three sectors depending on the erosion geometry:

Path motion and orbiting at radius = 0
Orbiting with radius > 0 scaled sector
Orbiting with radius > 0 in equidistant sector

Notice

The flushing motion is always carried out implicitly with a non-linear velocity profile.

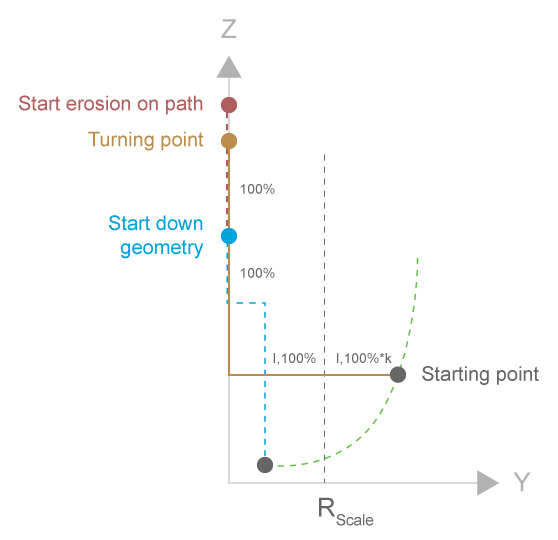
Classifying the dynamics of the flushing motion

Path motion and orbiting at radius = 0

In the case of path motions and orbiting at radius = 0, the escape channel has all the data required about which axes are moved - the orbit channel has no influence on moving axes. On the path, the escape geometry is a 3D geometry and at radius = 0 there is only motion along the Z axis in the Z/R coordinate system of the down and escape channels. For this reason, these motions can be traversed with maximum dynamics.

Orbiting at radius > 0 in the scaled sector

At radius > 0, the orbit channel moves the real electrode position in a plane perpendicular to the Z axis of the coordinate system in the escape channel. However, the escape channel only moves the Y and Z axes in its coordinate system, but has no data about the axes that are actually moved. For this reason, the dynamics of this motion is limited to 100% of the dynamics of the weakest axis.

Orbiting at radius > 0 in the equidistant sector

In linear corner elements of the equidistant sector, the actual distance traversed can be greater than the change in radius of the escape motion.
If the orbit channel is exactly in the corner, the factor k between the actual distance and the change in radius is sent by the orbit channel to the escape channel. The dynamics of the escape motion is then calculated at 100% dynamics of the weakest axis multiplied by the factor k. This results in a motion that is traversed at 100% dynamic of the weakest axis when the orbit channel is positioned exactly at the corner of the corner element.

If the orbit channel is not positioned exactly on the corner, the motion is less dynamic. The motion always stops at the transition to the scaled sector.