Permitted orbit geometries in “Equidistant” mode

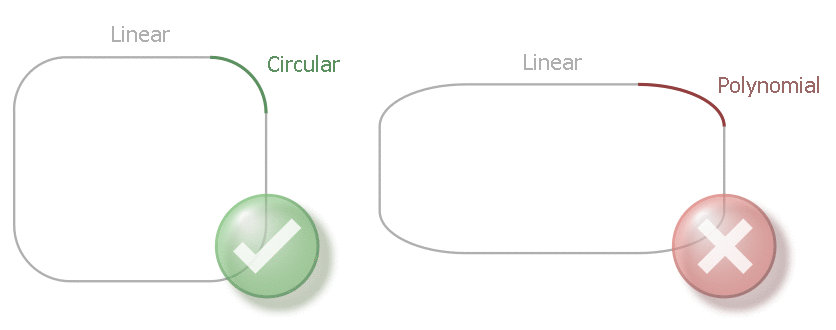
In “Equidistant” mode, the geometry may only consist of linear and circular elements. No polynomial elements are permitted.

Notice

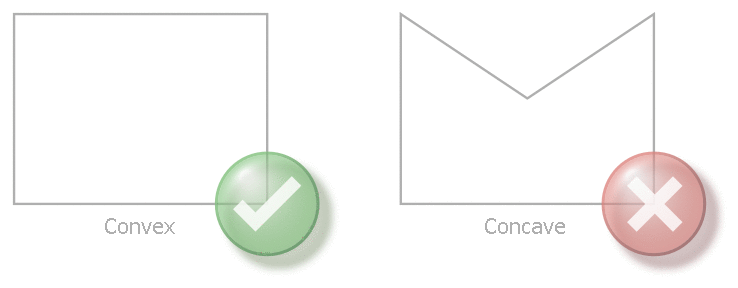
Geometries must be convex.

If geometries are concave, error ID 50918 is output.

The origin (0/0) must lie within the scaling range of the orbit channel. The positions of the origin are shown below:

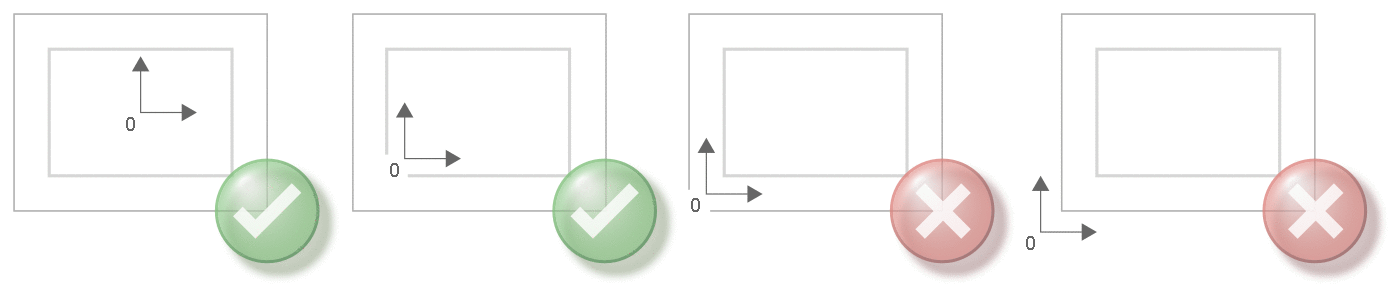
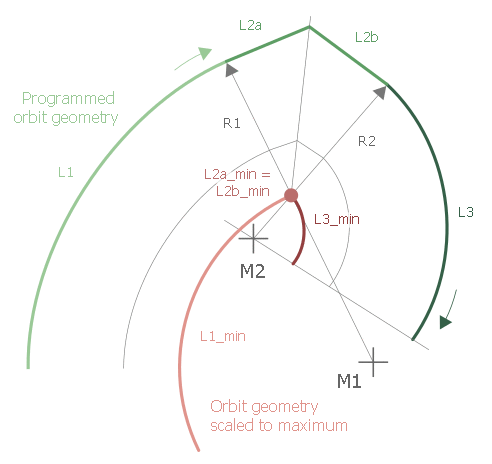
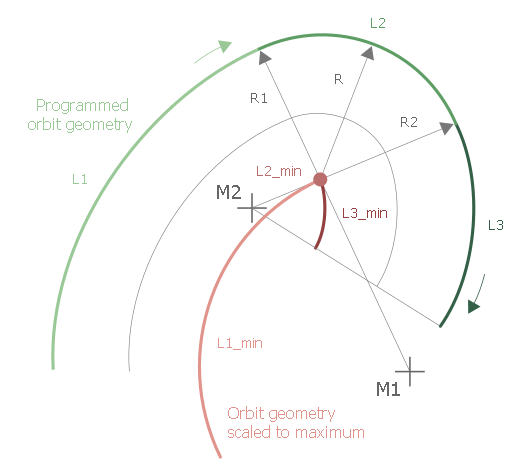
The equidistant is always calculated on the inside (cf. left/right tool radius compensation, G41/G42) for the specified orbit geometry. This is based on the direction of rotation of the orbit channel which is automatically defined by the direction of the programmed geometry. The centre of rotation (clockwise) is at coordinate (0/0):

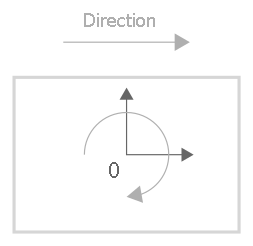
Transitions between two geometries

When an equidistant is calculated, there are certain limiting conditions that apply to the transitions between linear/circular blocks.

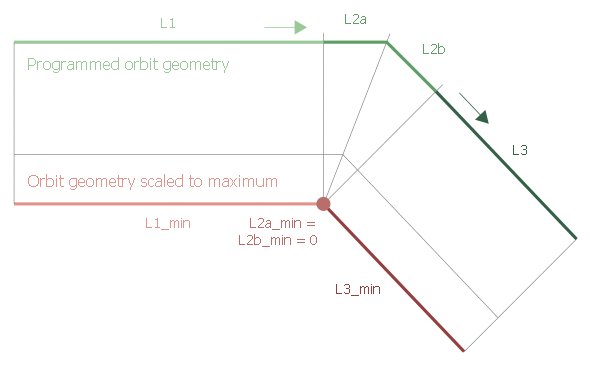
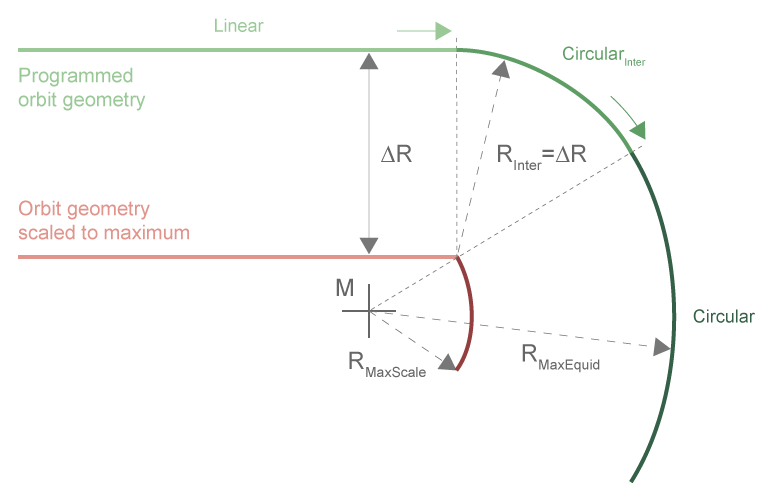
A non-tangential transition between two elements, as shown in the figure below, requires two linear elements of defined length at the break point. The length of the elements is:

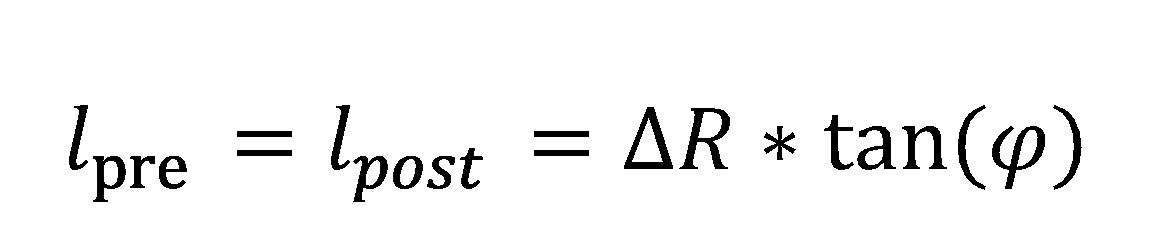
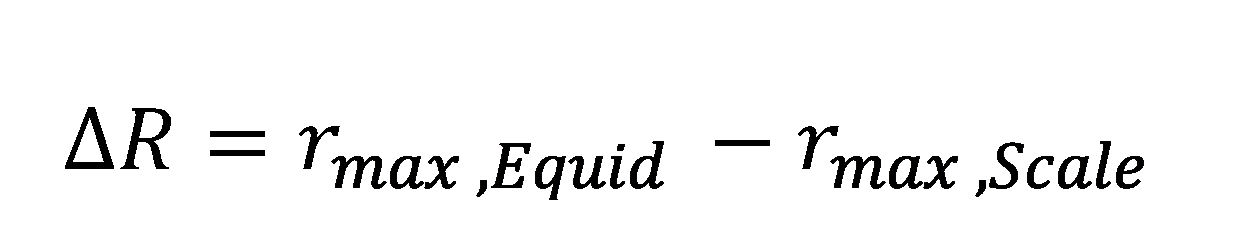
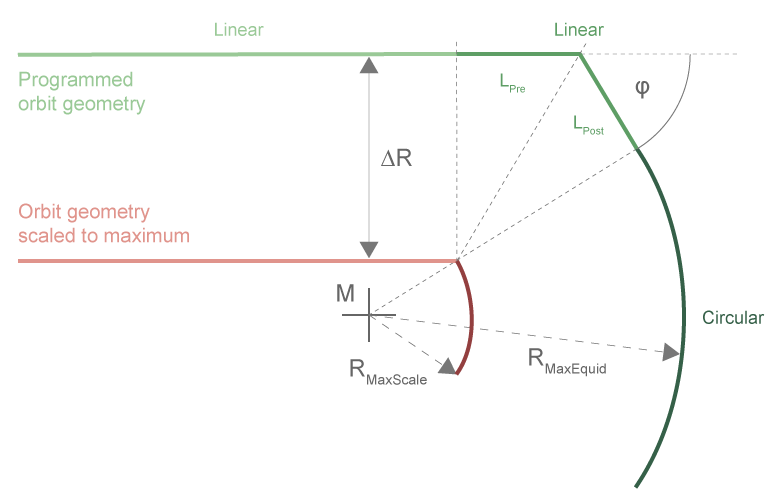
Notice

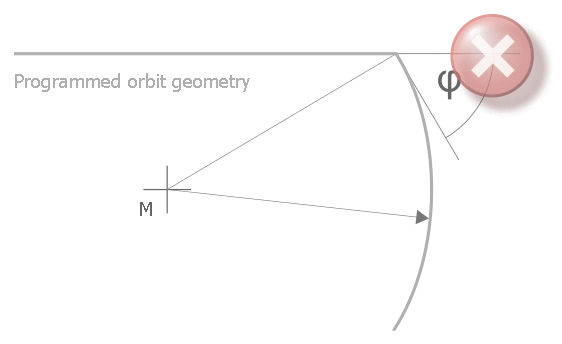
Every transition to a circular element must be tangential.

If transitions to circles are non-tangential, error ID 50914 is output.

Based on the above requirements for orbit geometry in equidistant mode, the following transitions between circular and linear elements are permitted:

Linear-linear transition:

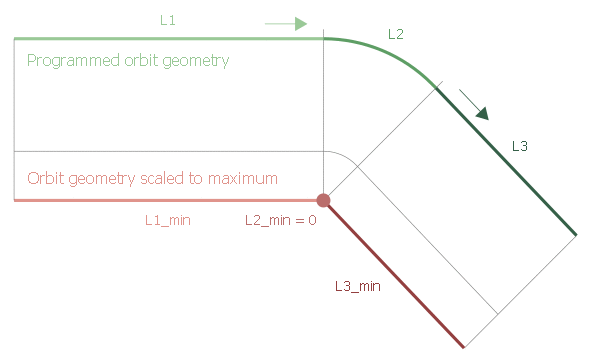
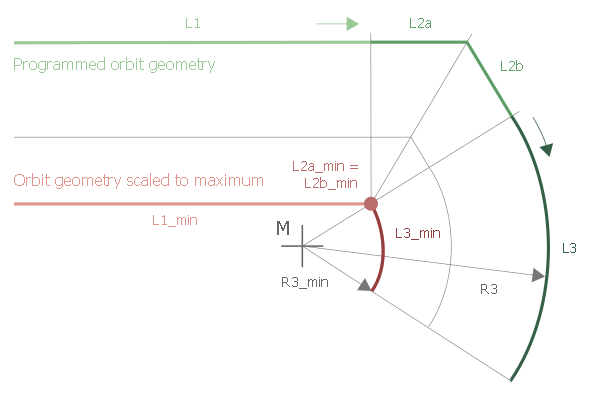
Linear-circular transition:

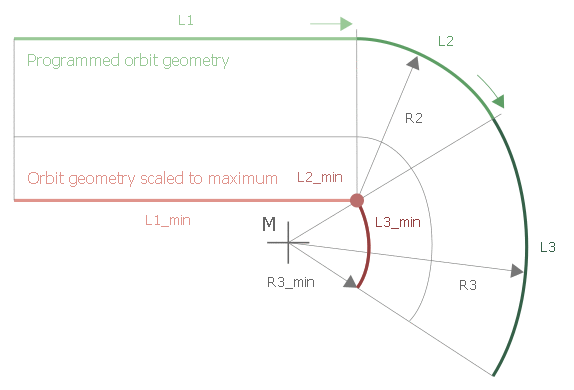
Circular-circular transition: